64=65？？？？？

まずはこの画像をご覧ください。

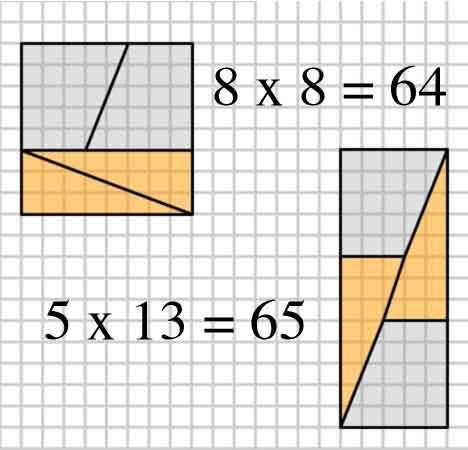
上の正方形の面積は8*8=64です

下の長方形の面積は5*13=65になります。

この2つの図形はそれぞれ2つの台形と2つの三角形に分解することができます。

そしてその台形と三角形を比較してみると・・・

なんと同じ大きさの三角形と台形ではありませんか！

ここでおかしいことに気がつきませんか？

同じ大きさの図形4つからできている正方形と長方形の面積が違うのです！

冷静になってもう一度考えてみましょう。

まずは台形の面積を求めます。

台形の面積の求め方は次の通り。

（上底＋下底）＊高さ÷２

この公式に当てはめると、この図形の中の台形は、

(5+3)*5÷2=20

台形は2つあるので、

20*2=40

ということになります。

次に三角形の面積です。

底辺＊高さ÷２

つまり、

3*8÷2=12

三角形は2つあるので、

12*2=24

台形と三角形の面積を足してみると、

40+24=64

あれ？やっぱり長方形の面積の65にならない。。。

ここで種明かしをしちゃいましょう。

まだ考えたい方は下のほうは見ないでくださいね。

実は、長方形の方の三角形は三角形ではないのです。

これは一種の錯視図形といってもいいでしょう。

この三角形はよく見ると底部の台形と上部の三角形が合わさったものなのです。

つまり四角形なのですよ。

定規をあてるなどして確認してみてください。

斜辺は直線ではないことに気がつくと思います。

では底部の台形と上部の三角形を分割して計算してみます。

底部の台形は、

(3+2)*3÷2=7.5

2つあるので、

7.5*2=15

上部の三角形は、

2*5÷2=5

2つあるので、

5*2=10

台形と三角形を足すと、

15+10=25

残った長方形の青い部分の台形の面積は40でした。

この2つの部分を足し合わせると、

40+25=65

はい、無事に最初の5*13=65と一致しました！

数学の問題に見えて、実は心理学的な問題だったのです。

こんな単純な図形なんですけど、人間の目って騙されやすいものなのですね。

実はとくとみもだいぶこの問題に悩まされました（笑）